重学操作系统笔记-1

“如何把程序写好”这个问题是可计算的吗？

公理化体系和不完备性定理

最早在 19 世纪初，德国著名数学家希尔伯特提出：这个世界可以建立一套完善的公理体系，由少数几个公理出发，推导出所有的定理和推论。这样就可以逐渐通过这种方法将世界上的万事万物都统一到一个体系中。

但在不久后，美籍数学家哥德尔就提出了哥德尔不完备性定理，内容是：即便在完善的公理体系中仍然可以找到不能被证明也不能被证伪的命题。

计算机能力也是有边界的。哥德尔的不完备性定理，让大家看到了世界上还有大量不可计算的问题。

图灵机和可计算理论

于是人们意识到了需要一个理论，专门回答这样的问题：哪些问题可以被计算，哪些不可以被计算，这就是可计算性理论，该理论是计算机科学的理论基础之一。

图灵发现如果一个问题是可计算的，那么它的解决方案就必须可以被具化成一条条的指令，也就是可以使用图灵机处理。因此，不能使用图灵机处理的问题，都是不可计算的问题。

比如一个马达的控制程序是可计算的，因为控制过程是可以被抽象成一条条指令的（即可以写程序实现）。比如程序可以先读入传感器的数据，然后根据数据计算出下面要进行加速还是减速。

不可计算问题

但当图灵机遇到“素数是不是有无穷多个？”这样的问题时，事情就变得复杂了。虽然，我们可以通过有限的步骤计算出下一个素数。比如可以每次尝试一个更大的数字，然后通过一系列计算过程判断该数字是不是素数，直到找到一个更大的素数。古希腊数学家埃拉托斯特尼就发明了筛选出给定范围内所有素数的方法。

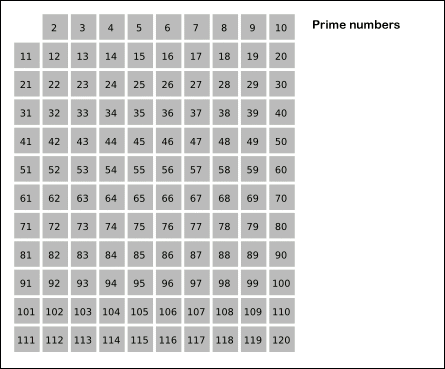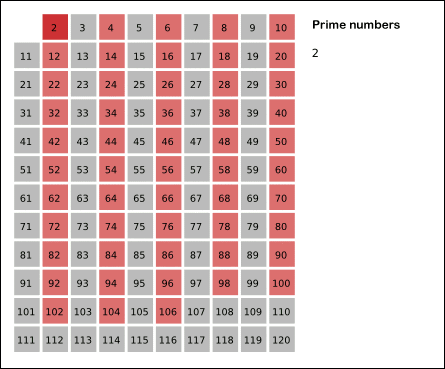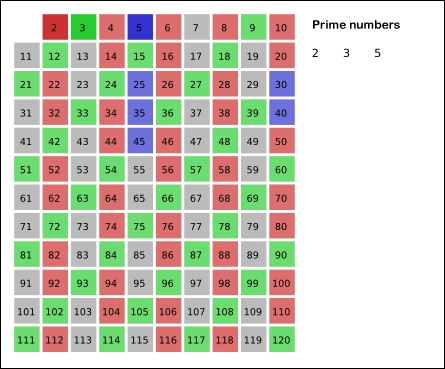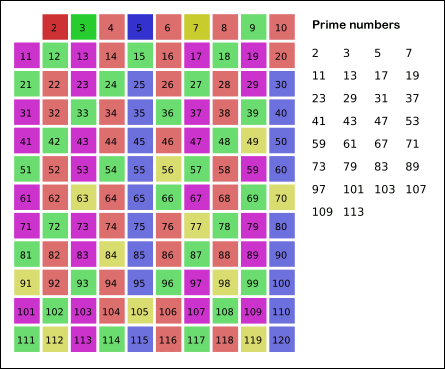
如上图所示，我们利用埃拉托斯特尼筛法找到的素数越来越多。但是，我们还是不能回答“素数是不是有无穷多个”这样的问题。因为要回答这样的问题，我们会不停地寻找下一个素数。如果素数是无穷的，那么我们的计算就是无穷无尽的，所以这样的问题不可计算。

停机问题

我们无法实现用一个通用程序去判断另一个程序是否会停止。不能因为这个程序执行了1天就判定它不会停止，也不能因为这个程序执行了 10 年，从而得出它不会停止的结论。这个问题放到图灵机领域，叫作停机问题，我们无法给出一个判断图灵机是否会停机的通用方法，因此停机问题是一个经典的不可计算问题。

回到最初的问题：“可不可以计算一个人程序写得好不好？”

虽然这个是一个不可计算问题，但是可以通过设立一些规则，比如：检查缩减、检查函数复用情况、检查类的命名情况等，给写程序的人更好的建议。另外，我们也可以通过 AI 技术，让机器在“程序写得好不好”这个问题的判定能力上，达到人类的水平，通过图灵测试。

相比 32 位，64 位的优势是什么？

32 位宽的CPU最多操作 23^2 个内存地址，也就是 2^32=4G，当然数据总线也是32条。但是64位的CPU并不意味着处理速度会比32位的快，因为在日常处理的数据中，比如一个用户的金额不会超过10万，而2^32约等于20亿，所以这样的计算一般是不会有什么却别的。而64位意味着可以操作更大的内存，更高速的通讯，所以在计算大数据时会比32位更有优势。